Cryptography – stream ciphers

Author:
Innokrea Team

Date of publication: 2023-11-30

Caterogies: Security

Today we want to tell you about how stream ciphers work, what LFSR registers are, and where we use such stream ciphers. If you’re interested in the low-level operation of encryption algorithms and other concepts closely related to cryptography, we invite you!

Introduction

To truly understand how individual encryption algorithms work, it’s important to realize that symmetric ciphers – those that use the same key for encrypting and decrypting messages – can be divided into block ciphers and stream ciphers. Block ciphers are primarily used on the Internet, while stream ciphers are used where resources are limited, such as in embedded systems or Bluetooth, although there are exceptions to this rule. Both of these approaches have their own advantages and disadvantages, as well as several subtypes with specific characteristics. Block ciphers combine fragments of plaintext bits with key bits to create a ciphertext of the same size. Stream ciphers, on the other hand, don’t directly combine plaintext bits with key bits; instead, they generate pseudorandom bits using a key and then perform XOR operations on them.

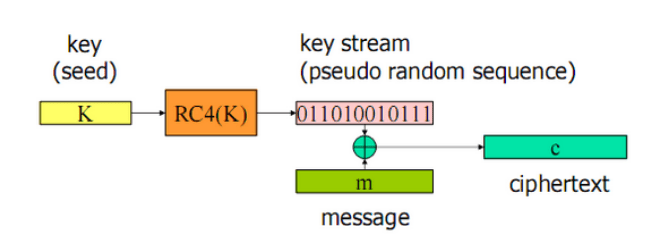
Figure 1 – Example of the RC4 stream cipher, source: wentzwu.com

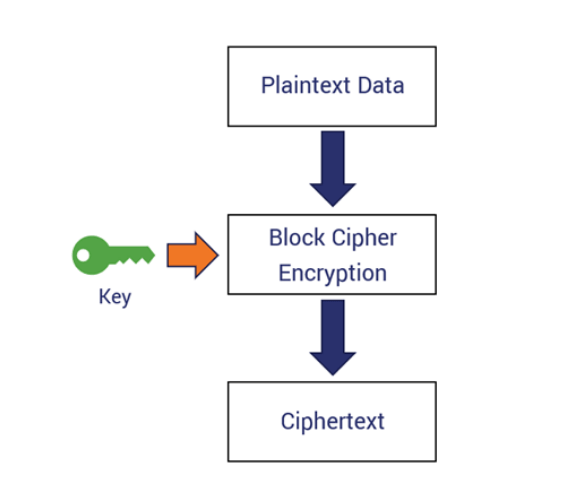
Figure 2 – Basic concept of a block cipher, source: thesslstore.com

Stream Ciphers – Basics

Stream ciphers, according to what we’ve mentioned and shown in the above Figure 1, encrypt bit by bit. They are similar to DRNG (Deterministic Random Bit Generator) which deterministically (meaning for the same input, the output is always the same) produce a sequence of bits from an initial value called the seed. Stream ciphers, however, take two values: the key and the nonce, where the key should be a secret value, and the nonce should be unique. This means there are certain limitations due to the size of the nonce value. If a value is 8 bits, for instance, there are 2^8 possible messages before we have to change the key. If we don’t do this, there’s a probability that if two identical messages appear, they would have the same ciphertext. Yet, the whole idea of encryption assumes that a potential attacker should not be able to infer any information about the message without possessing the key.

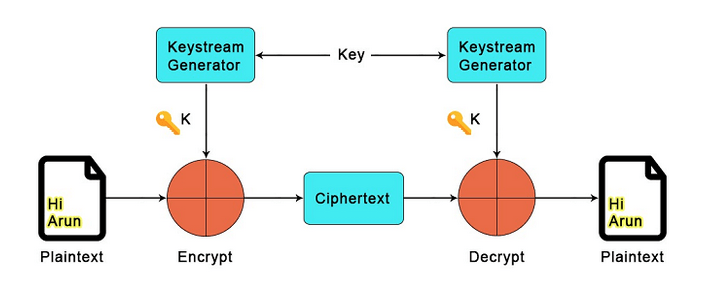
Figure 3 – Operation of a stream cipher, source: javatpoint.com

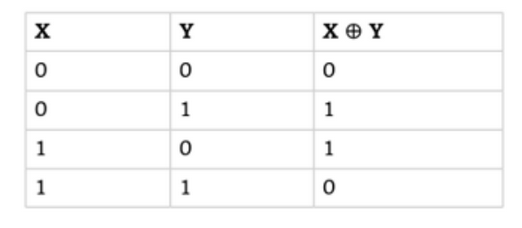
After generating pseudorandom characters, the stream cipher algorithm performs an XOR operation on the plaintext. Let’s take a moment to examine the truth table for this operation and its specific properties.

XOR has an interesting property that allows for result inversion, meaning if c = p ⊕ k, then c ⊕ k = p ⊕ (k ⊕ k) = p ⊕ 0 = p.

This can even be seen in the truth table. Imagine that X is a bit of plaintext, and Y is a bit from the generated pseudo-random cipher sequence – so X ⊕ Y is the ciphertext. If X = 0 and Y = 1, then X ⊕ Y = 1. Now, if we want to reverse this operation, taking Y = 1, from the truth table we see that X ⊕ Y = 1 results in 0. The operation is therefore reversible.

This property, among others, means that for stream cipher algorithms, separate encryption and decryption functions aren’t needed, because it’s the same XOR operation that is reversible.

Types of Stream Ciphers

There are several types of stream ciphers, and they can be categorized in various ways. The basic classification includes two categories:

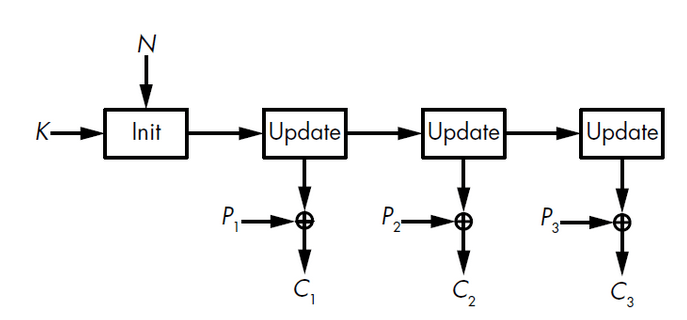
Stateful stream ciphers – the stream possesses an internal state that changes during the stream generation process, e.g., RC4, Salsa20.

Figure 4 – Stateful stream cipher, source: Aumasson, Serious Cryptography

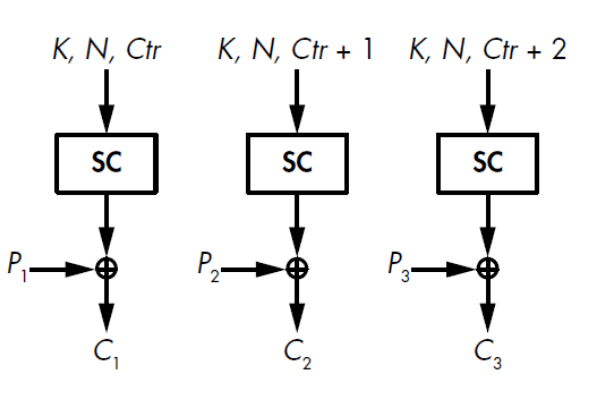
Counter-based stream ciphers – the stream lacks an internal state, which is replaced by a counter incremented with each step. N is the nonce, which should be unique for each applied key (important for key rotation).

Figure 5 – Counter-based stream cipher, source: Aumasson, Serious Cryptography

LSFR

Closely related to the concept of a stream cipher is the idea of an LFSR (Linear Feedback Shift Register). It’s a shift register whose input bit is a linear function of its previous state, used for generating random values for stream ciphers (keystream). Proper usage of such a generator exhibits strong statistical properties; however, this doesn’t necessarily mean that such a register possesses appropriate cryptographic properties.

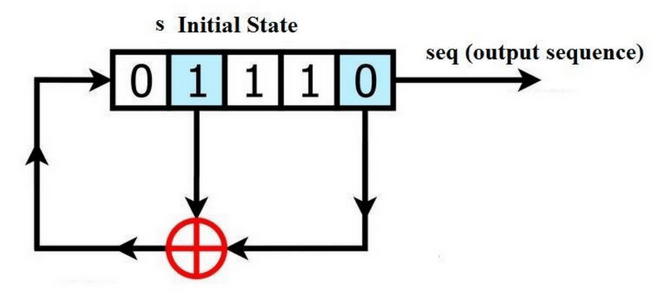
Figure 6 – Structure of an LFSR shift register, source: minutesheep

Shift registers of this type, with XOR operations on certain bits, create looped bit representations of numbers generated by the register. For example, a given 4-bit register loops in a cycle of 16 possibilities (which is the optimal value, the maximum), generating binary numbers from 0000 to 1111. In practice, such registers are longer and are represented in polynomial form, where the number of bits in the register is the highest power of the polynomial.

These polynomial-represented registers can then be optimized through mathematical transformations to maximize the length of cycles. This is done because different XOR combinations of different bits yield different effects. For example, it’s possible to create a 128-bit shift register connected in a way that it generates only numerical values from 0 to 15 in the last 4 bits. However, this is suboptimal, as it means the generated keystream will have a length of 4 bits, which is weak and equivalent to using a 4-bit register. An optimal polynomial, meaning one with a maximum cycle, must satisfy certain mathematical properties, including being a primitive polynomial (refer to sources below). Tables of classified primitive polynomials can be found readily available on the Internet.

Security of LFSR

Despite the fact that the algorithm for obtaining random bits possesses good statistical properties, it’s not the best from a cryptographic standpoint. In LFSR registers, output and state bits are linked by “m” linear equations, which can be solved using clever mathematical and computational techniques. In practice, cryptography employs additional cryptographic mechanisms to enhance the LFSR concept cryptographically. Filtered LFSR registers or nonlinear FSR (NFSR) registers are used. These introduce additional transformations that render the linear equations mentioned earlier nonlinear, making them either impossible or difficult to solve.

Where Are Stream Ciphers Used For?

There are many places where we use stream ciphers, including:

Older versions of Bluetooth (up to 3.0, which used the E0 cipher, now considered unsafe)
Older versions of Wi-Fi security (WEP used the RC4 cipher, also now considered unsafe)
TLS (various stream cipher algorithms like RC4, ChaCha20 – some considered safe, others not; we recommend referring to the RFC documentation)
GSM mobile telephony (A5 algorithm, currently considered unsafe)

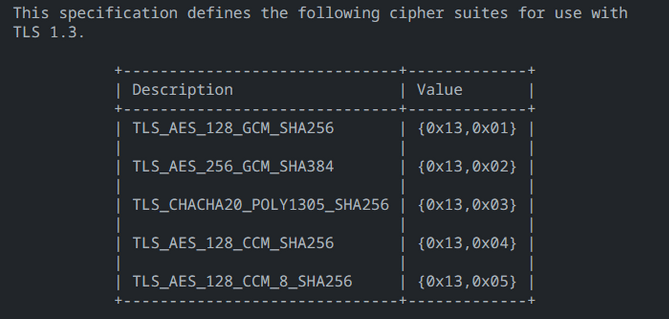
Figure 7 – Possible security mechanisms for TLS 1.3 – both block ciphers and stream ciphers like ChaCha20

Are Stream Ciphers Faster and More Efficient?

The answer is: it depends! In theory, stream ciphers should be faster due to the smaller number and lower complexity of operations. However, this depends on various factors such as implementation, key length, or input data length. Nonetheless, modern optimized implementations like AES, through dedicated processor instructions and hardware accelerators, can achieve similar or even greater speeds when using the appropriate block cipher mode.

When it comes to encryption efficiency, it refers to the amount of resources, such as memory, bandwidth, or power, used during the encryption process. Efficiency is important in situations where resources are constrained, such as in embedded systems, wireless networks, or mobile devices. Stream ciphers exhibit higher efficiency compared to block ciphers, generally having less code, using less memory, and generating less communication overhead. Consequently, stream ciphers result in lower energy consumption due to fewer computations and less heat generation. Block ciphers require more resource allocation both during implementation and operation.

Summary

As you can see, low-level topics related to encryption are not easy at all. Next week, we will briefly move away from the cryptography topic and focus on other aspects of computer science. See you then!

Sources:

See more on our blog:

User Identity and Access Management – What’s the Deal with IDP?

What user identity is? Why managing access is essential for businesses? How an IDP (Identity Provider) works? You will find the answer to these questions in the article.

Security

2024-12-11