Innokrea Team is presenting a new episode of the supercomputers series, where we will tell you about the organization of network architecture in cluster systems, network topologies, graph theory, and what else to consider when building such systems. Enjoy reading!

 

Interconnect Systems

Interconnections are crucial in supercomputers because computational applications require parallel processing of enormous amounts of data, often across thousands or even millions of individual computing elements. This is important because data movement is the most costly operation in parallel systems in terms of performance.

To achieve the desired level of parallelism, supercomputers utilize specialized interconnections that provide high-bandwidth communication and low latency between individual computing elements. An essential element influencing these parameters is the network topology, which describes the structure used to connect processors and switches.

There are several different types of interconnections commonly used in supercomputers, including InfiniBand, Ethernet, and proprietary interconnections developed by vendors such as Cray and Fujitsu.

 

Network Systems - Basic Components

The interconnect network consists of the following elements:

  • Endpoints - Endpoints are the sources and destinations of messages, in our case, the processors.
  • Switches - A switch is a device connected to a fixed set of links. It forwards received packets to one or multiple links.
  • Links - Cables used to transmit data between endpoints and switches, as well as between switches. It should be noted that in the case of distributed memory systems, the nodes (endpoints) are equipped with a network interface card responsible for sending and receiving data from the network on behalf of the main processor.

 

Direct vs. Indirect Networks

A significant division in computer networks for supercomputers is whether the network is built based on direct or indirect connections. This may seem a bit strange to people familiar with everyday network devices such as switches and routers because we build home or corporate networks based on intermediary devices. Let's look at the definitions first:

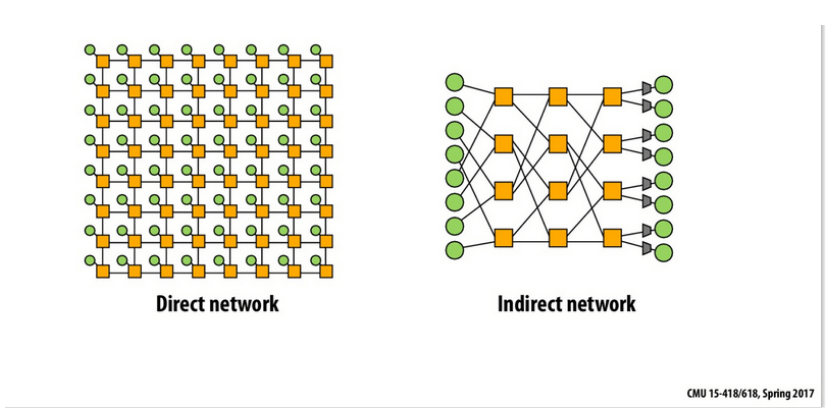
  • Direct network - In a direct network, a node acts as both an endpoint and a switch.
  • Indirect network - In an indirect network, endpoints are connected via switches.

Figure 1: Comparison of indirect and direct networks, where green represents computing units (processors), and yellow represents intermediary devices.
In the case of a direct network, these combined devices are merged into one. Source: Carnegie Mellon University.

 

Supercomputers can be built using both direct and indirect networks. This depends on the technology and topology employed.

 

Network Topology and Graph Theory

The branch of mathematics known as graph theory is closely related to network topologies and the construction of optimal networks, particularly in supercomputers where the number of nodes is enormous and delays must be minimized. A network can be represented as an undirected graph, where vertices represent nodes and edges represent network connections. It is undirected because messages can be transmitted in both directions. We want connections to exist between any two nodes. When characterizing a connection, we consider parameters such as:

  • Diameter (D) - the maximum distance between any two nodes, indicating the maximum possible delay in the network when there is no contention for the medium. Distance is defined as the shortest path between two nodes.
  • Degree - the degree of a vertex in a graph (the number of incident edges) is a good indicator of the hardware cost of a particular installation (higher degree = higher cost).
  • Bisection Bandwidth - the minimum number of vertices that need to be removed to divide the network into two equal-sized networks. It tells us about the maximum achievable throughput when n/2 communications are initiated simultaneously in a system containing n processors. Note that to calculate the effective bisection bandwidth, one must multiply the number of links by their bandwidth.

 

Direct Network Topologies

The aforementioned parameters from graph theory are used to determine the characteristics of a network and how well it suits a supercomputer or another high-performance system.

 

Sources for illustrations are available at the very bottom. They have not been included alongside the images to avoid cluttering the concepts.

Figure 2: Ring.

 

Degree: 2

Diameter: ⌊n/2⌋

Bisection bandwidth = 2

 

Not used in supercomputers.

Figure 3: Mesh (Clique).

Degree: n-1

Diameter: 1

Bisection bandwidth = ⌊n/2⌋ * ⌊n/2⌋

 

The mesh is optimal in terms of performance, but it is also very expensive as the number of edges increases with the number of nodes. It is rarely used in practice in supercomputers.

Figure 4: W-Dimensional Mesh.

Degree: 4

Diameter: 2 * ⌊√n - 1⌋

Bisection bandwidth = √n

 

This topology is well-suited for problems in a 2-dimensional space, such as image processing. In the diagram, each node serves as both a switch (yellow color) and an endpoint (green color). It is classified as a direct network topology.

Figure 5: W-Dimensional Torus.

 

Degree: 4

Diameter: 2 * ⌊√n/2⌋

Bisection bandwidth = 2 * √n

 

The torus offers a smaller diameter and larger bisection bandwidth compared to the W-dimensional mesh at a similar cost. It is a topology commonly used in supercomputers.

 Figure 6: Fat-tree.

 The Fat-Tree topology is a tree-based topology. Processors are the leaves of the tree, and all other nodes in the tree are switches. The key characteristic of a Fat-Tree is that each switch in the Fat-Tree has the same number of incoming and outgoing links. This can be interpreted as links becoming thicker, i.e., having greater bandwidth, toward the root of the tree. It is a topology used in intermediate networks (with switches) in supercomputers.

 

A Fat-Tree of the nth level can be costly in practice because the switches toward the root of the tree become larger. However, there is an alternative solution that involves using only a set of switches with the same capacity. It should be noted that such a solution is, in fact, a spine-leaf topology. The tree then consists of two levels of switches.

Such a Fat-Tree is very popular in practice due to its relatively low hardware cost. However, the maximum size of such a network is limited by the number of ports in the switches used in the network.

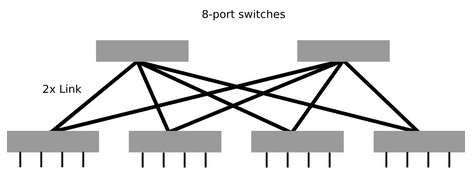
Figure 7: Two-Level Fat-Tree.

 

For a two-level Fat-Tree, the dependencies can be calculated using the following formulas:

  • Number of second-level switches = k/2
  • Total number of switches = k + k/2 = 3k/2
  • Maximum number of nodes = k²/2

Where k is the number of ports in a switch. Additionally, for a two-level Fat-Tree, the parameters Diameter and bisection bandwidth are:

  • Diameter = 4
  • Bisection bandwidth = ⌊n/2⌋

These are good parameters - small diameter and high bisection bandwidth, making it a topology commonly encountered in supercomputers, especially those related to Infiniband technology.

 

Topologies are the subject of scientific research, and their context in parallel programming is also studied. Here's an example of a conference paper on supercomputers, where the authors propose optimizations related to MPI in the context of the dragonfly topology.

Figure 8: Dragonfly Topology vs. MPI.

 

This is the penultimate entry in the series on supercomputers. As you can see, the topic is quite complex and encompasses an entire branch of science, involving computer specialists ranging from programmers to network experts, as well as mathematicians striving to propose theoretical improvements. In the next article, we will tell you about Infiniband and RDMA, which are specific technologies used to increase speed and reduce latency in high-performance systems. 

 

Sources: