FastAPI – how to write a simple REST API in Python? – part 1
REST API in Python? Nothing easier. Start your FastAPI adventure with us today!
 Author:
Author:Last week in our ML series, we introduced the process of training artificial neural networks—its phases, data splitting, and the importance of monitoring the training process. Today, we want to delve deeper and analyse what happens inside a neural network during a single training epoch. Let’s get started!
First and foremost, it’s essential to note that while the general concept of training neural networks is relatively consistent, there are many variations. Today, we will discuss one of the simplest methods—adjusting the model’s weights and biases after each individual sample from the training dataset is presented (in the literature, this approach is known as stochastic gradient descent – SGD).
With that said, let’s explore what happens inside a neural network during a single training epoch:
Steps 1-4 are often referred to as the forward pass, and steps 5-6 are known as the backward pass.
It’s essential to pay attention to one more aspect of neural network architecture. While hidden layers can contain any (within reason) number of neurons, it is common to choose powers of 2 for their size. However, when it comes to input and output layers, there are some specific rules to follow:
Let’s take a jump back to the figure from one of our previous articles of this series:
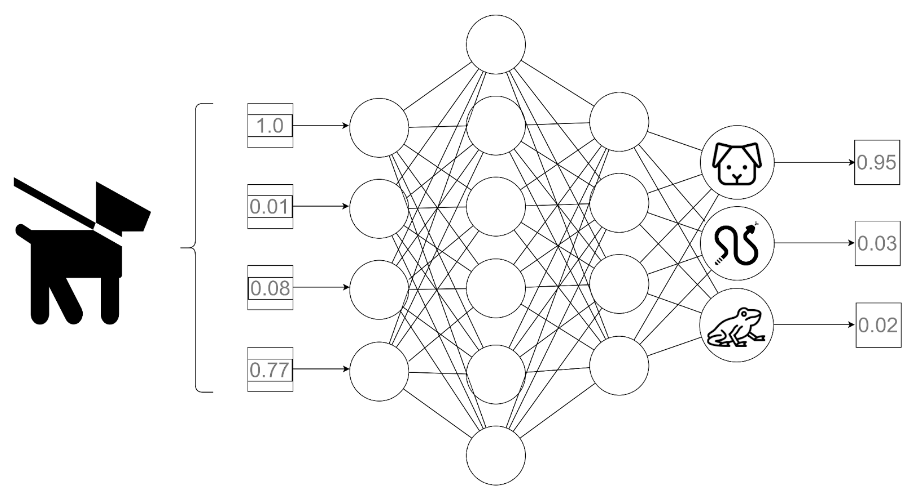
Fig. 1: A simplified example of a forward pass
Now, let’s take a closer look at what happens during the forward pass through the hidden layers of the network:
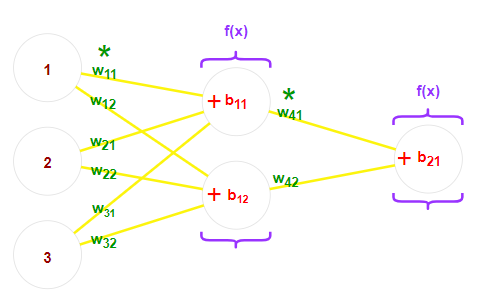
Fig. 2: A close-up look on neural networks parameters: weights are green, biases are red (roses are too), activation functions are purple.
Notice that the operations conducted so far (multiplication and addition) linearly modify the input values. If we continued to treat data this way, each subsequent layer would be a linear transformation of the previous layer’s output. This output is, in fact, a result of linear operations. Mathematics leaves no doubt in this regard—composing linear functions, regardless of their number, is still just a linear function! It means that without introducing activation functions that break the linearity of our structure, the entire complex neural network could ultimately be replaced by… a single function of the form f(x) = ax + b. While linear functions are surprisingly powerful statistical tools, constructing them through elaborate, artificial neural networks might sound a tiny bit like an overkill.
Now, let’s talk about activation functions:
f(x) = max(0, x).
This function maintains linear dependence for values greater than or equal to zero, while rounding off all negative values to zero.
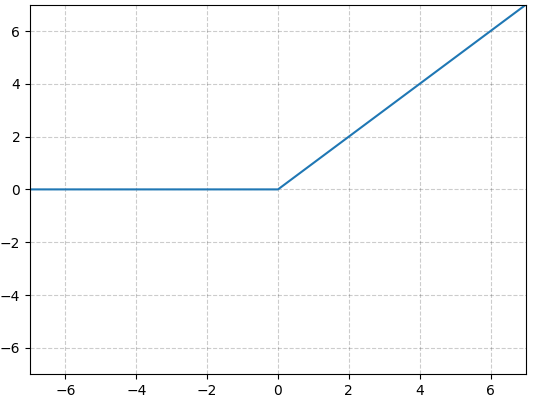
Fig. 3: Plotted ReLU
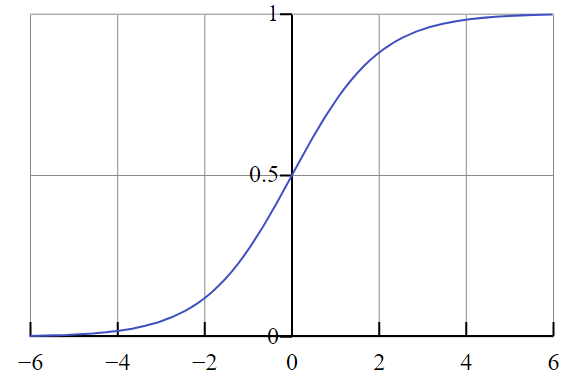
Fig. 4: Plotted sigmoid (src: Wikipedia.org)
We’ve achieved results; now it’s time to check how far they are from the truth. The loss function helps us determine how much error our network has made by comparing the obtained results with the ground truth. Commonly used loss functions include cross-entropy and categorical cross-entropy, but delving into the mathematical details is beyond the scope of this article.
The final step in the parameter adjustment phase of an epoch is backpropagation. It involves calculating the derivative of the loss function for each parameter in the network. This derivative tells us in which direction and to what extent each weight or bias should be adjusted to bring the result closer to the truth. After computing this multi-dimensional derivative (the gradient) for all trainable network parameters, their values are updated (how drastically depends on the chosen learning rate).
That’s all for today! See you next week when we’ll take a closer look at how the training could be improved and how do neural networks look from a cybersecurity perspective. Take care until then!

FastAPI – how to write a simple REST API in Python? – part 1
REST API in Python? Nothing easier. Start your FastAPI adventure with us today!
Programming
2024-07-18

Dockerizing the frontend – do it right with React.js + Vite
Do it right! A guide to dockerizing React.js with Vite.
Programming
2024-07-04
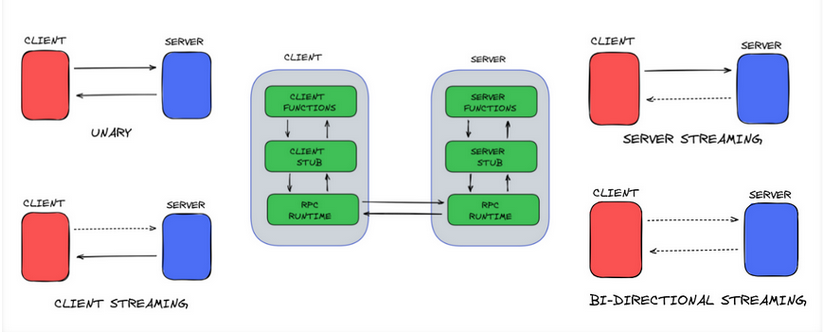
On Processes, Protobuf, and RPC
A bit about RPC, serialization, interprocess communication, and how it relates to distributed systems.
AdministrationProgramming
2024-06-20