Cryptography – randomness in cybersecurity

Author:
Innokrea Team

Date of publication: 2023-11-02

Caterogies: Security

Today we want to talk to you about randomness in cryptography. What is randomness, how to accurately estimate it, and how crucial it is in the field we’ve dedicated our recent articles to. If you’re interested, we invite you to read on!

Randomness – Is It That Important?

Why does cryptography concern itself with the concept of randomness? The answer to this question is quite simple. It does so because randomness forms the foundation of most concepts within the entire field of cryptography: in key generation, so-called salts, initialization vectors, as well as in encryption systems and even during attacks on cryptographic systems. If cryptographic operations are predictable, and thus non-random, it means that those actions are inherently unsafe.

Intuition Fails

Intuitively, our minds seem capable of determining whether a certain sequence of characters is random. However, in the case of long character sequences, such as 128-bit keys, this is practically impossible. Furthermore, during intuitive reasoning about randomness, we typically make two types of mistakes:

We assume something is random because it looks random, and our brain doesn’t detect any pattern in it.

We assume that behind apparently random patterns, there must be some pattern or scheme.

In practice, to obtain sequences that are random, we use a branch of mathematics related to probability and statistics (probability distributions). Processes occurring in nature or experiments have certain probability distributions. For example, if we toss a fair coin with a probability of ½, we get heads, and with a probability of ½, we get tails. The probability distribution adds up to 1, because according to the definition of probability, a value of 1 means certainty of occurrence (1 represents 100% probability). The probability distribution of flipping a fair coin is uniform, as each event (heads and tails) is equally likely (½). When generating consecutive zeros and ones in cryptography, you can think of them as successive coin tosses.

Distinguishing sequences that appear random from those that are truly random is the foundation of security in cryptography. Using pseudorandomness instead of true randomness undermines the entire cryptographic system at its core.

Entropy – Measure of Uncertainty

According to the definition, to formally define this, we’ll need the concept of a probability distribution, which assigns probability values to individual events in a random process. For example, the coin toss distribution is ½ probability for heads and ½ for tails. The probabilities in the distribution must add up to a value of 1 (according to the definition of probability).

Entropy, on the other hand, is a measure of uncertainty or disorder in a system. The greater the entropy, the greater the uncertainty about the outcomes.

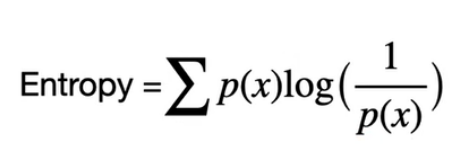
Figure 1 – Sum of probabilities of individual events multiplied by “surprise measure.” The logarithm has a base of 2 (binary logarithm) – this is the so-called Shannon entropy.

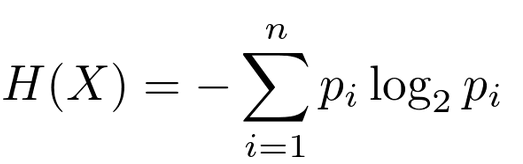
Figure 2 – More commonly encountered form of the formula from Figure 1, source: towardsdatascience.com

The second term in the formula, log(1/p(x)), can be seen as a measure of our surprise. For example, if we perform tosses with an unfair coin where the probability of getting heads is ⅛ and tails is ⅞:

Entropy = ⅛ * log(1/(⅛)) + ⅞ * (log(1/(⅞))) = ⅛ * 3 + ⅞ * 0.193 = 0.375 + 0.169 = 0.544

If we get heads, our “surprise” is 3, and if we get tails, it’s only 0.193. This is because we expect heads less, as the probability of such an event is relatively small (surprise is inversely proportional to the probability of the event).

Let’s consider an example of entropy in a fair coin:

Entropy = ½ * log(1/(½)) + ½ * log(1/(½)) = ½ * 1 + ½ * 1 = 1

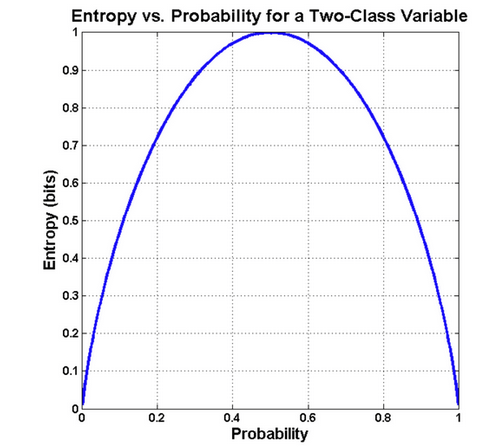
Figure 3 – Entropy function for a coin toss depending on the chosen probability distribution. – source: bytepawn

In the figure, we can observe that the highest entropy (measure of uncertainty) is for a uniform distribution, where event probabilities are equal (½ for each side of the coin). Entropy is maximal when the distribution is uniform because no result is more likely than others.

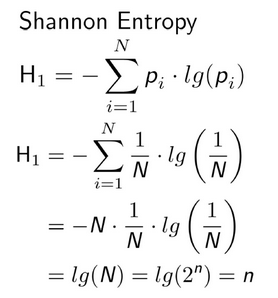
Figure 4 – The entropy formula can be simplified for a uniform distribution as follows (pi = 1/N, N = 2^n (n bits)), source: osti.gov

This means that for a key of, let’s say, 128 bits in cryptography, whose generator has a uniform distribution, the entropy is n bits.

Let’s think for a moment about an 8-byte (64-bit) password. Such a password can have a maximum entropy of 64 bits. Intuitively, to have reasonable chances of cracking this password, one would need to randomly try half of those possibilities, which is equivalent to 2^64 / 2 = 2^63 combinations. This amounts to 9.223372e+18 attempts. However, if we assume that the password could be a dictionary word, the possibilities decrease to just a few hundred thousand. In this case, we have a non-uniform distribution because words used in language are more likely than those that appear random, resulting in lower entropy. This can significantly ease the process of cracking such a password. This is why, to ensure the highest possible protection for our data, we should use password generators (often part of password managers) instead of using easy-to-remember but unsafe dictionary words.

Imagine a scenario where we want to send our secret password to a friend, and to do so, we encrypt it with a pre-shared key (PSK). Someone intercepts our message and tries to guess the key. If our generated password has low entropy (for instance, it’s a dictionary word), an attacker attempting to decrypt the ciphertext with a certain key will easily conclude that they found the correct key and possess the correct password. On the other hand, if the original message had high entropy, then after decrypting with multiple guessed keys, the message will still not be readable for a human (it won’t be any “meaningful” word) – thus, we won’t be certain if it’s the actual text we are looking for. This example makes sense only if the attacker knows the key length and the key length is shorter than the length of the transmitted message.

OTP – One-time pad

The above example about entropy also illustrates why a cipher with a one-time pad key is secure. This type of cipher is essentially the same as the Caesar cipher, but with each letter/bit having a different key value. This means that for each message, we’d need a unique n-bit key (so, for encrypting a 500 GB disk, we’d need a 500 GB key). While this cipher isn’t practical, it’s important to understand why it’s referred to as a cipher of perfect secrecy. If an attacker has unlimited computational power, they cannot guess the original text even with a brute-force attack, as shown by Claude Shannon in the 1940s.

One could use a vivid example by Francis Litterio (link to his full article in the description).

“If the key is truly random, an XOR-based one-time pad is completely resistant to a ciphertext-only attack. This means that an attacker cannot deduce the plaintext from the ciphertext without knowledge of the key, even through brute-force searching of the key space. All possible plaintexts are equally likely.”

Assuming that you intercepted a very small, 8-bit ciphertext. You know that it’s either the 8-bit ASCII character ‘S’ or the ASCII character ‘A’, encrypted with a one-time pad. You also know that if it’s ‘S’, the enemy will attack by sea, and if it’s ‘A’, the enemy will attack by air. That’s a lot of information. All you’re missing is the key, a simple little 8-bit one-time pad. You instruct your team of cryptanalysts to try all 256 possible 8-bit one-time pads (2^8 combinations), which is a brute-force attack. The result of searching the key space is that your team finds one 8-bit key that decrypts the ciphertext to ‘S’ and one that decrypts it to ‘A’. And you still don’t know which one is the actual plaintext. This argument can be easily generalized to keys (and plaintexts) of any length.”

Although OTP is theoretically perfect, its practical implementation faces many challenges. Generating truly random keys of the same length as the message is difficult. Additionally, securely sharing and managing such long keys can be logistically complex. However, you can read about historical uses of OTP, including by KGB spies, on Wikipedia (link in sources).

True Random Number Generators (TRNG) vs. Pseudo-Random Number Generators (PRNG)

At the core of the security of cryptographic systems lies randomness, as we’ve already established. We’ve learned that the highest entropy is achieved with a uniform distribution. However, how can we generate a number that is truly random? A certain component is needed, one that serves as the source of randomness. For this purpose, we need two types of RNG (Random Number Generator):

TRNG (True Random Number Generator) – source of entropy
PRNG (Pseudo Random Number Generator) – cryptographic algorithm that generates high-quality random bits from the entropy source

The source of entropy can be a component that draws from an analog environment, that is, something unpredictable, using parameters like temperature, acoustic noise, electricity, or mouse movement. TRNG generates bits in a non-deterministic way without a guarantee of high entropy; it’s slow and not on demand. Additionally, in nature, many phenomena have a Gaussian distribution, which is not a uniform distribution. Therefore, there must be a mechanism to transform the probability distribution into a more uniform one. This process is called post-processing and is the subject of extensive research.

PRNGs, on the other hand, rely on TRNGs and, after obtaining a few random bits from TRNG using algorithms and advanced mathematics, transform the source into a long stream of reliable, random bits. The PRNG generator receives the bits obtained by TRNG at regular time intervals into a buffer and generates a new sequence in a deterministic manner. The combination of these two approaches enables us to ensure adequate randomness and to make our keys unique, resulting in cryptographic systems being secure as well.

Are we really safe?

In 2012, researchers conducted an analysis of certificates and public keys on the Internet from SSH and HTTPS services. It turned out that many systems had identical or similar keys because the algorithms used there relied on the same random factors. These factors were generated at the system’s startup when the RNG hadn’t yet obtained sufficient data to ensure proper entropy. Differences in keys arose from additional entropy added programmatically using PRNGs, but this was a reversible process. We recommend familiarizing yourself with the article below, especially page 13, where advice for developers is described. See you in a week!

https://www.usenix.org/system/files/conference/usenixsecurity12/sec12-final228.pdf

Sources: