Green Data Centers – How to Choose an Eco-Friendly IT Partner?
A Guide for Companies Looking for IT Providers Using Energy-Efficient Infrastructure and Renewable Energy
 Author:
Author:Today we want to tell you about hash functions, hashes, and later about passwords – their storage and generation. We’ll try to start with the basics and gradually serve you more complex knowledge on this topic. If you’re interested, we invite you to read on!
Hash functions are mathematical functions that, when given a string of any length, return a string of fixed length, for example, 256 bits. Each input string produces a unique output string. Hashing is an operation that results in the loss of some information, as we can process a long string into one of fixed length. Additionally, it’s worth mentioning that hashing is irreversible (or at least it shouldn’t be reversible), meaning that knowing the hash should not allow us to determine the original input.
Examples of hash functions include MD5, SHA-1, SHA-256, SHA-3, or BLAKE. Hash functions are used for:
Every internet user unknowingly uses various hashing mechanisms while connecting via VPN, accessing websites with locks (SSL/TLS), or programming using version control systems (hashes of individual commits). Even antivirus programs check virus signatures (which is why hackers use polymorphic viruses); these signatures are essentially calculated by passing the virus code (whole or part) through a hash function.
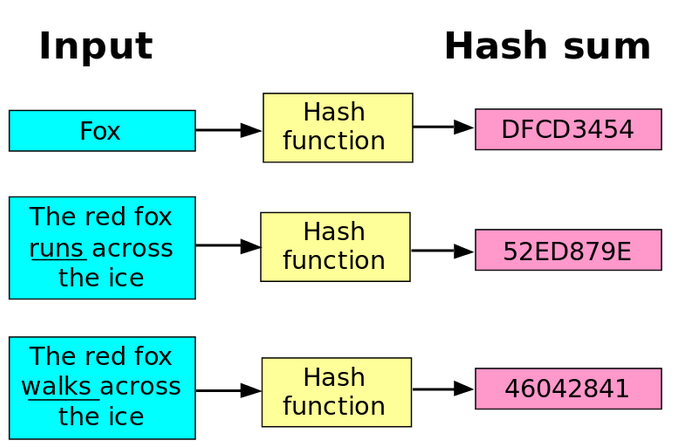
Figure 1 – Hash function operation, source: commons.wikimedia.org
It’s also important to note that not every hash function is suitable for cryptographic applications. For example, cyclic redundancy checks (CRC) are used for integrity verification in networks and do not provide any cryptographic security. In summary, while data encryption aims to provide confidentiality, hashing functions are meant to ensure data integrity, i.e., to prove that data hasn’t changed during transport.
A very common use of hash functions is in digital signatures, where after calculating the hash of a message, it is encrypted with its private key. The recipient decrypts the hash using the sender’s public key and then calculates the hash of the received message. If the values match, it means the message hasn’t been altered and was sent by the person possessing the corresponding private key. Signing the hash of a message is as secure in terms of integrity as signing the whole message. Most signature algorithms can work only on short data, i.e., message hashes, which is an optimal solution
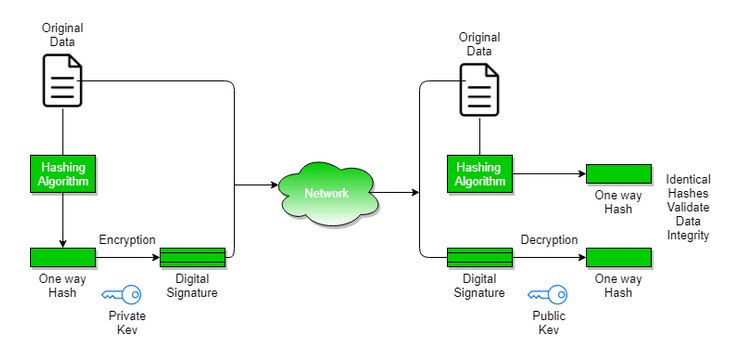
Figure 2 – Sending a digitally signed message and signature verification, source: geeksforgeeks
The concept of a hash function relies on its randomness and unpredictability. A well-designed hash function should:
Hashes and cryptography are also connected to the so-called Birthday Paradox. The problem is as follows: How many people must be gathered in a room for the probability of two people having their birthdays on the same (any) day to be over 50%? The answer is surprising. Despite a year having 365 days, only 23 people are needed for this, and with 57 people, there’s already a 99% certainty of two of them sharing the same birthday. How is this possible? If you’re interested in the mathematical details behind this paradox, we recommend this 3-minute video: https://www.youtube.com/watch?v=Y_shcEgdhI8
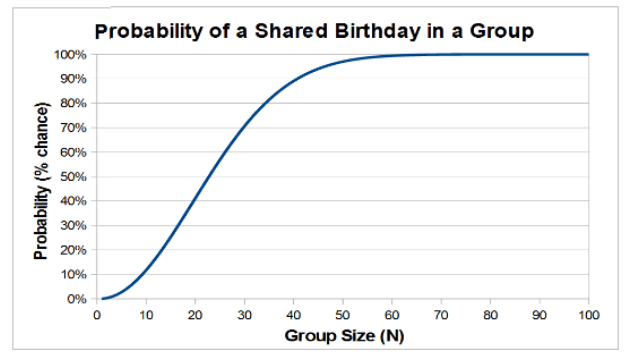
Figure 3 – Probability chart of the same birthday depending on group size, source: edscave.com
In hashing, the birthday paradox also finds its application. If we consider the number of days in a year as the number of possibilities to represent different numbers on N bits, i.e., 2^N, we can estimate how many hashes we would need to check to find two inputs of a hash function producing the same hash. Using an online calculator like https://www.bdayprob.com/, we can say that for a 16-bit hash (2^16 = 65536 possible different hashes), only 300 hashes are needed to have a 50% chance of finding a collision.
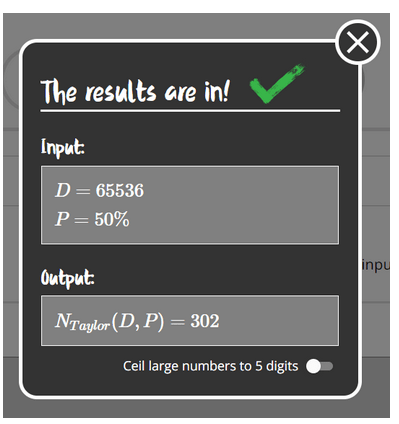
Figure 4 – D – number of days in a month (in our case, the number of possible hashes), P – probability of collision we want to achieve, Output – minimum number for achieving 50% success rate
What if we consider this situation for a 256-bit hash? A 256-bit sequence can be constructed in approximately 2^256 ways, which is about 10^77. To achieve 50% success, one would need to generate 4*10^38 hashes.
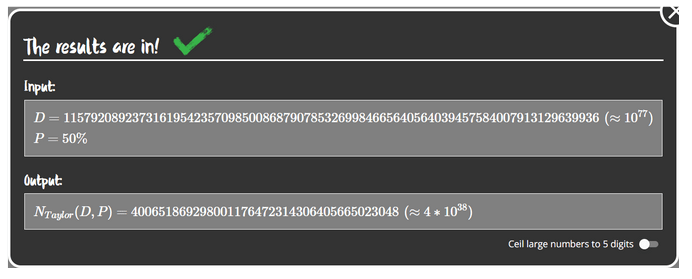
Such enormous numbers are not intuitive for humans. Let’s ask how long it would take to find such a hash, assuming we have the computing power of the Bitcoin network, which is around 500 exahashes/s (500 * 10^18).
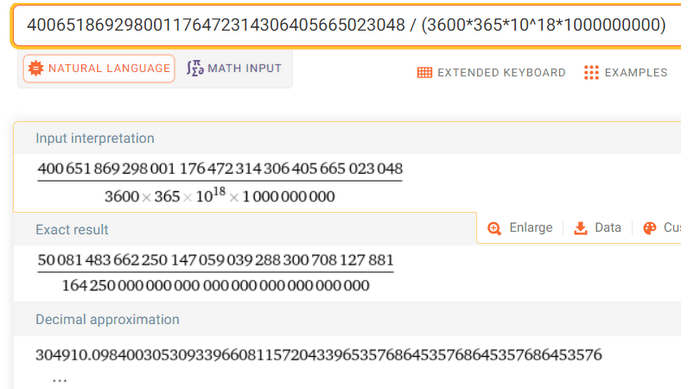
Taking these values into account, generating such an amount of hashes would take 305,000 billion years, which is thousands of times greater than the age of the entire universe. We should also ask what portion of all 256-bit hashes needs to be generated to hypothetically achieve this effect. It’s 1/(4 × 10 ^ -39) * 100% (10^34 times less than a per mille). This means that even if it’s such a tiny fraction of all hashes that would need to be generated, today’s computational power capabilities do not allow for it – and let’s remind that the whole solution concerns finding collisions between any two input chains and does not account for sorting, searching, and storing such a massive amount of data.
In short, a properly designed 256-bit hash function is more than secure according to today’s computational power standards.
There are also more optimal collision search methods that do not require as much memory and computation, and one of them is the Rho method. It works as follows:
This method uses less memory than naive storage and searching of random values. Typically, finding a collision requires about 2^(n/2) + 2^(n/2) computations, where n is the number of bits.
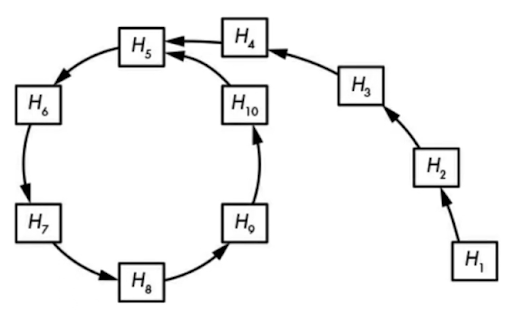
Diagram – visualization of the Rho method, where successive arrows represent the calculation of subsequent hash values. The loop indicates a found cycle, and the inputs H10 and H4 produce the same output – H5. Source – Jean Phelippe Aumasson – Modern Cryptography
We hope that today’s mathematical considerations didn’t overwhelm you. Next week, we’ll continue delving a bit more into hashing topics and explore their practical applications. Until then!
Sources:

Green Data Centers – How to Choose an Eco-Friendly IT Partner?
A Guide for Companies Looking for IT Providers Using Energy-Efficient Infrastructure and Renewable Energy
Green IT

Helm for the Second Time – Versioning and Rollbacks for Your Application
We describe how to perform an update and rollback in Helm, how to flexibly overwrite values, and discover what templates are and how they work.
AdministrationInnovation

Helm – How to Simplify Kubernetes Management?
It's worth knowing! What is Helm, how to use it, and how does it make using a Kubernetes cluster easier?
AdministrationInnovation